Shader入门精要读书笔记(前置知识)
Shader入门精要读书笔记——前置知识
数学篇
- 二/三维笛卡尔坐标系
- 左手坐标系和右手坐标系
- 点和矢量
- 矩阵、矩阵运算、特殊矩阵
矩阵的几何意义:变换
在游戏开发中,三维(二维)物体的变换即是矩阵的可视化方式。这里的变化一般包括:平移、旋转和缩放。例如Unity中的Transform即包括了这三个属性。
什么是变换?
变换指将数据(位置、方向、甚至颜色等)通过计算进行转换的过程。
变换中的一个重要类型是线性变换,线性变换指满足以下两个条件的变换:
$f(x)+f(y)=f(x+y)\quad(1)$
$kf(x)=f(kx)\quad(2)$
上面提到的旋转和缩放就是线性变换。
值得注意的是,平移并非线性变换,如我们从点(1, 1, 1)进行2次(1, 2, 3)的平移,代入上(1)式,得
$f(1,2,3)+f(1,2,3)=(4,6,8)$
$f((1,2,3)+(1,2,3))=(3,5,7)$
可见两式结果并不相等,因此我们不能仅使用3x3的矩阵来表示上面的所有变换。
齐次坐标
为了表示所有变换,我们将3x3的矩阵扩展到4x4的矩阵,相应地,点和方向的向量也需要从三维矢量扩展到四维矢量,扩展后的坐标便称为齐次坐标。
我们把点和方向扩展到四维向量时,按以下方式填充它们的第四维元素w(这么填充的原因在后续变换时可以看到):
$点向量 P(x,y,z)—->P(x,y,z,1)$
$方向向量 D(x,y,z)—->D(x,y,z,0)$
变换矩阵
所有的变换矩阵都可以表示如下
$
\left[
\begin{matrix}
M_{3×3} & t_{3×1} \\
0_{1×3} & 1 \\
\end{matrix}
\right]
$
其中左上角的M用作缩放和旋转,右上角的t用作平移。
平移矩阵
平移矩阵如下,左右分别为对点和向量的计算结果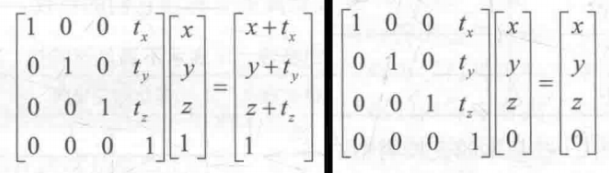
可见平移矩阵对点产生了正确的偏移,而不会对方向产生影响。
平移矩阵的逆矩阵即右上的t部分取符号相反。
平移矩阵并非正交矩阵。
缩放矩阵
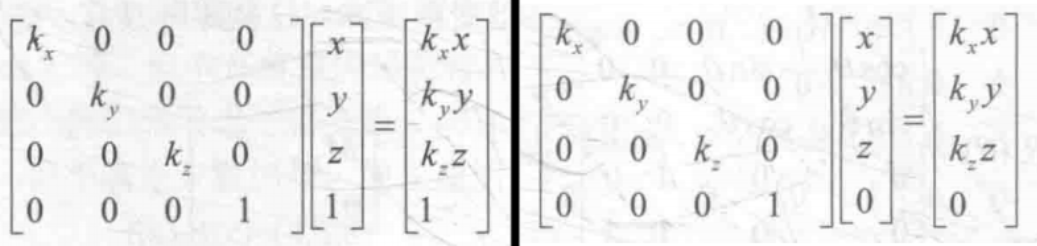
缩放矩阵对点和方向均会产生影响。
缩放矩阵的逆矩阵即每项取倒数。
缩放矩阵并非正交矩阵。
缩放系数 $k_1=k_2=k_3$ 的称为统一缩放(uniform scale),否则称为非统一缩放(nonuniform scale)。
- 注意,非统一缩放会改变与模型相关的角度,如后续提到的法线变换。
旋转矩阵
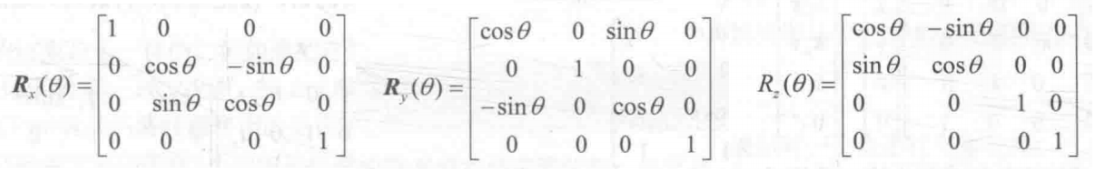
旋转矩阵分别根据物体绕的坐标轴,可以分为3部分。
复合变换
不同的变换可以通过矩阵乘法来进行组合,如
$
P_{new}=M_{translation}M_{rotation}M_{scale\theta}P_{old}
$
这里我们如上述图中使用的都是列矩阵,阅读顺序为从右到左,因此这里变换的顺序为先缩放,再旋转,再平移,这是符合直觉的(如果先平移,再缩放,则缩放会把平移的位移进一步缩放)。
这里的矩阵顺序必须严格按照变换顺序来计算,其根本原因是矩阵乘法不满足交换律。
坐标空间
在游戏开发中,我们需要用到很多不同的坐标系。
为什么要用那么多坐标系?
因为不同场合使用不同的坐标系方便。所有坐标系理论上都是平等的,只有方便/麻烦之分,而没有对错之分。
坐标空间的转换
已知子坐标空间C的三个坐标轴在父坐标空间P下的表示$x_c,y_c,z_c$,以及原点位置$O_c$,当已知一个子坐标空间下的点$A(a,b,c)$,我们可以得到
$A_p=O_c+ax_c+by_c+cz_c$
$A_p=(x_{oc},y_{oc},z_{oc})+\left[
\begin{matrix}
x_{xc} & x_{yc} & x_{zc} \\
y_{xc} & y_{yc} & y_{zc} \\
z_{xc} & z_{yc} & z_{zc} \\
\end{matrix}
\right]
\left[
\begin{matrix}
a \\
b \\
c \\
\end{matrix}
\right]$
为了去掉这个加号(即平移),我们将其扩展到齐次坐标下
$A_p=(x_{oc},y_{oc},z_{oc}, 1)+\left[
\begin{matrix}
x_{xc} & x_{yc} & x_{zc} & 0 \\
y_{xc} & y_{yc} & y_{zc} & 0 \\
z_{xc} & z_{yc} & z_{zc} & 0 \\
0 & 0 & 0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
a \\
b \\
c \\
1 \\
\end{matrix}
\right]$
$=
\left[
\begin{matrix}
1 & 0 & 0 & x_{oc} \\
0 & 1 & 0 & y_{oc} \\
0 & 0 & 1 & z_{oc} \\
0 & 0 & 0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
x_{xc} & x_{yc} & x_{zc} & 0 \\
y_{xc} & y_{yc} & y_{zc} & 0 \\
z_{xc} & z_{yc} & z_{zc} & 0 \\
0 & 0 & 0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
a \\
b \\
c \\
1 \\
\end{matrix}
\right]$
$=
\left[
\begin{matrix}
x_{xc} & x_{yc} & x_{zc} & x_{oc} \\
y_{xc} & y_{yc} & y_{zc} & y_{oc} \\
z_{xc} & z_{yc} & z_{zc} & z_{oc} \\
0 & 0 & 0 & 1 \\
\end{matrix}
\right]
\left[
\begin{matrix}
a \\
b \\
c \\
1 \\
\end{matrix}
\right]$
$=M_{c->p}P_A$
于是我们便得到了从坐标空间C转换到坐标空间P的变换矩阵$M_{c->p}$。
现在我们只取左上角的3x3矩阵作为讨论,来求从P到C的变换矩阵。
因为坐标轴均为单位向量,所以$M_{c->p}$是一个正交矩阵,其逆矩阵等于其转置矩阵。
所以我们有
$M_{p->c}=M^{-1}_{c->p}=M^T_{c->p}$
$=\left[
\begin{matrix}
x_{xc} & y_{xc} & z_{xc} \\
x_{yc} & y_{yc} & z_{yc} \\
x_{zc} & y_{zc} & z_{zc} \\
\end{matrix}
\right]$
这样我们就求出了从P空间转换到C空间的变换矩阵。
常用的坐标空间
模型空间(Model Space)
我们拿到的模型(网格数据Mesh),其中的顶点均是以模型坐标系存储的。
模型空间有时也被称作对象空间(Object Space)或局部空间(Local Space)。
世界空间(World Space)
世界空间是我们处理计算机图像时接触到的最大的坐标系,且其只有一个。
从模型空间变换到世界空间,本质上就是对每个顶点进行平移,旋转,缩放的过程。
其变换矩阵如下
$M_{model}=M_{translation}M_{rotation}M_{scale\theta}$
所以我们有$P_{world}=M_{model}P_{model}$
观察空间(View Space)
观察空间即摄像机空间(Camera Space),是以摄像机(也就是观察者)为原点的空间坐标系。
- 如何得到顶点在观察空间的坐标?
- 计算观察空间的3个坐标轴在世界空间下的坐标,运用前述方法计算出世界空间到观察空间的变换矩阵。
- 想象相机在世界空间下的变换过程,即先旋转后平移,我们用逆变换将其回到世界空间原点,就相当于把所有世界空间中的顶点变换到观察空间下。
显然,两者得到的结果是完全相同的
裁剪空间(Clip Space)
裁剪空间的目的是对顶点进行裁剪,以此来判断那些顶点需要被显示,那些顶点因为在屏幕外而需要被裁剪。
这里的”屏幕外“由视锥体决定,最常用的是透视投影和正交投影,来定义2种不同的视椎体,效果如下图。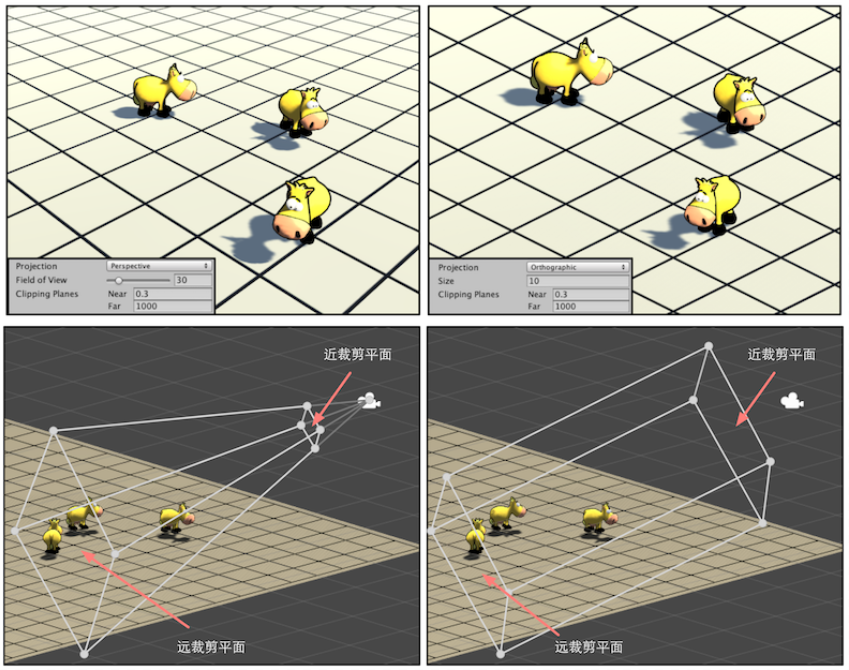
- 这个矩阵有什么用呢?
我们用这两种投影矩阵变换世界空间下的坐标后,将会得到一组新的$(x, y, z, w)$坐标,这组坐标将会让我们在裁剪顶点时计算更方便。正常地裁剪,我们需要判断一个顶点的坐标是否被视椎体的6个平面包围,这个计算的消耗太大;而变换后,我们只需要用x,y,z分别与第四个分量w作比较即可。
如下图是透视矩阵以及变换后的顶点坐标
如下图是透视矩阵变换后的关键顶点的坐标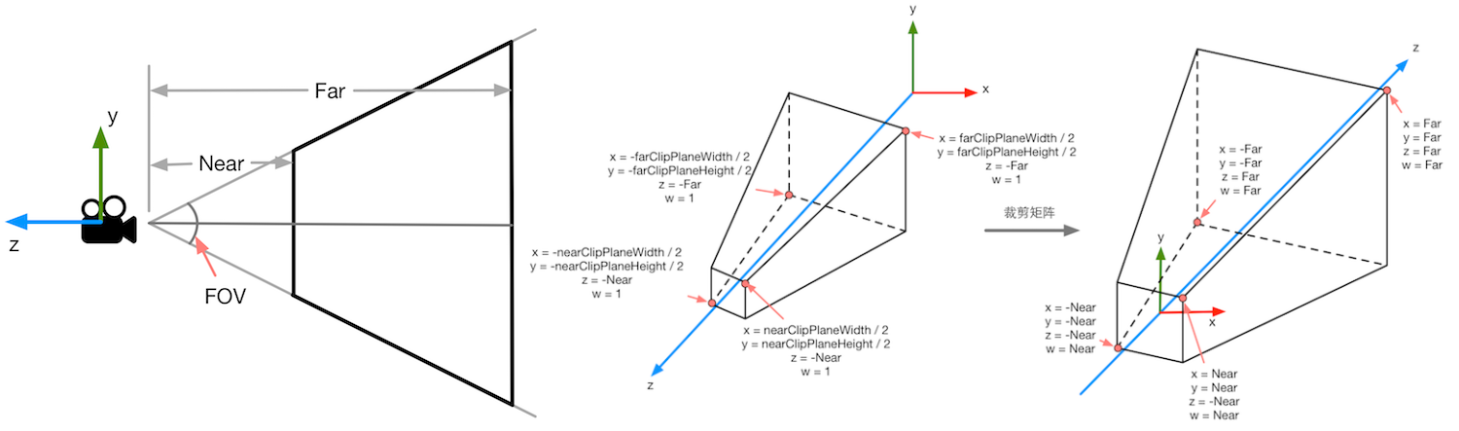
如下图是正交矩阵以及变换后的顶点坐标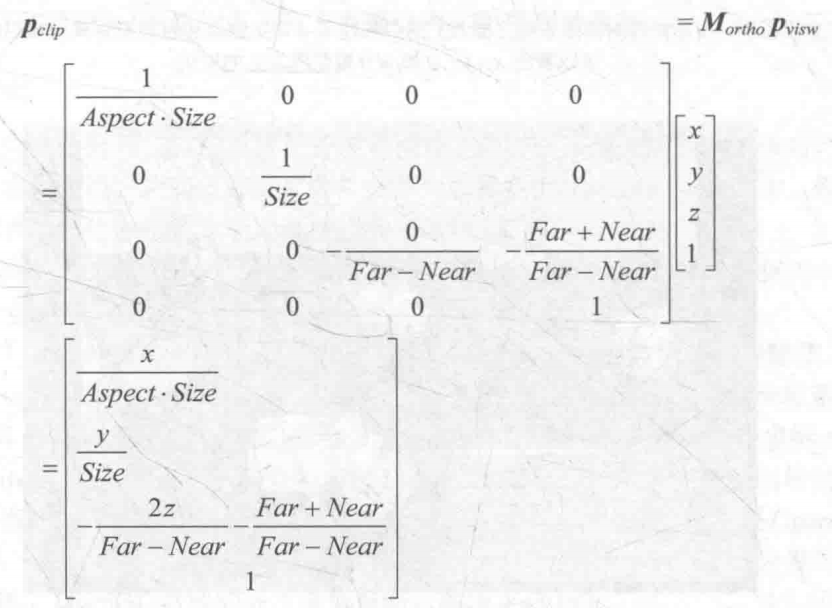
如下图是正交矩阵变换后的关键顶点的坐标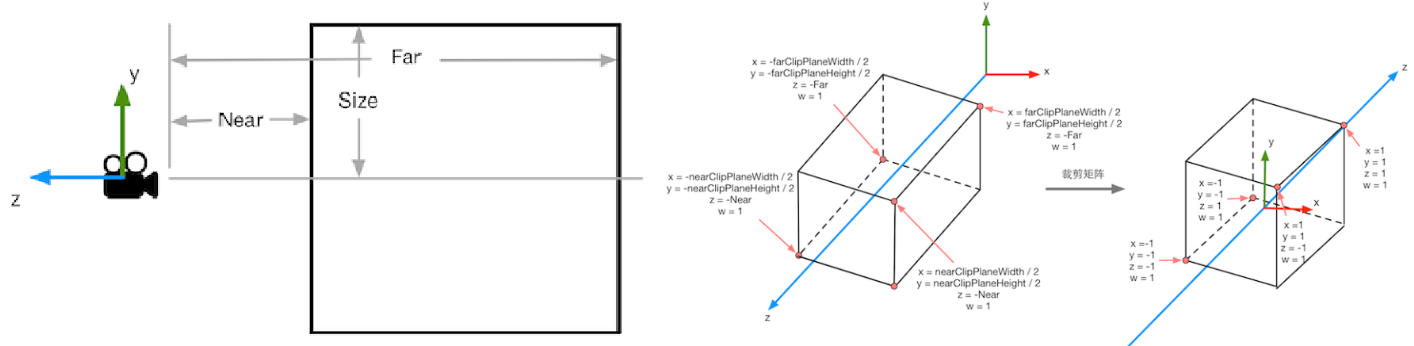
屏幕空间(Screen Space)
屏幕空间坐标,即二维坐标,是显示器上的像素位置,其范围是$(0, 0)—(Screen_{Width}, Screen_{Height})$。
经过上一步的投影矩阵变换,现在我们计算屏幕空间坐标就变得非常简单了。
将上一步的x,y分别除以w分量后,我们得到了2个范围在(-1,1)的分量(注:OpenGL中这个值是(-1, 1),而DirectX中这个值的范围是(0, 1)),我们将这个范围remap到屏幕分辨率即可。
值得注意的是,这里的z分量除以w后,一般情况下都被用作了深度缓冲,这个值的范围是(0, 1)。深度缓冲将被用作深度检测等地方。
- 重要的是,注意到上述透视矩阵变换后的顶点坐标,我们将z除以w分量后可以得到:
$\frac{Far+Near}{Far-Near} + \frac{2*Near*Far}{z(Far-Near)}$
简化换元后为
$k\frac{1}{z}+C$
可以看到,经过透视矩阵转换后,Z的值与转换前并非线性关系,即深度值非线性的。
此外,正交矩阵并不存在这个问题。
如下图,为变换后的深度值随原Z坐标变化的曲线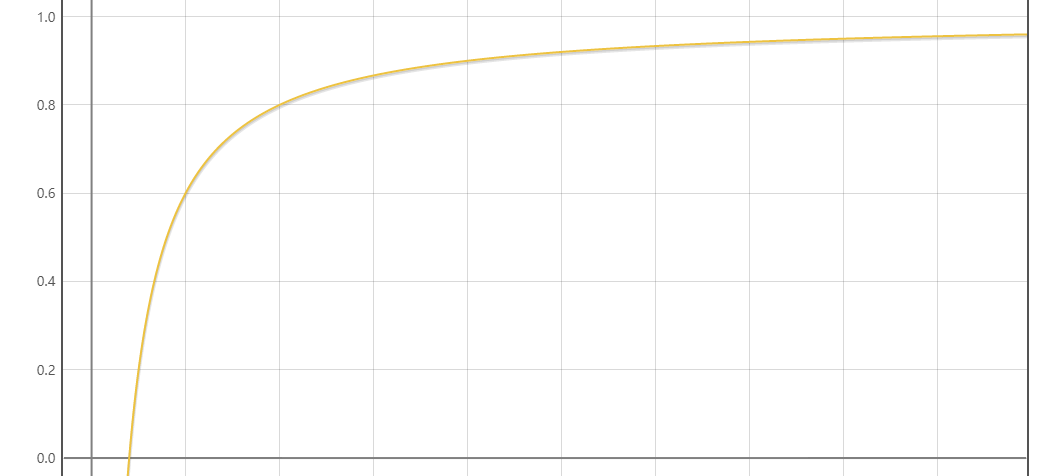
后续
在一系列变换之后,片元(fragment)还需要通过一系列测试,如深度测试,模板测试等之后,才可以正式将颜色着色在该像素上。
此外,在着色的时候,也有着许多不同的混合方式,如不透明物体会将自身颜色直接替换掉当前像素的颜色缓冲,并更新深度值;而透明物体会将自身颜色与颜色缓冲中的颜色值进行混合,这里的混合又有多重计算方式,如常见的计算方式是
$Color_{Final} = Alpha * Color_{Fragment} + (1 - Alpha) * Color_{Origin}$
总结
这里整理一下上述提到的渲染管线的整体流程如下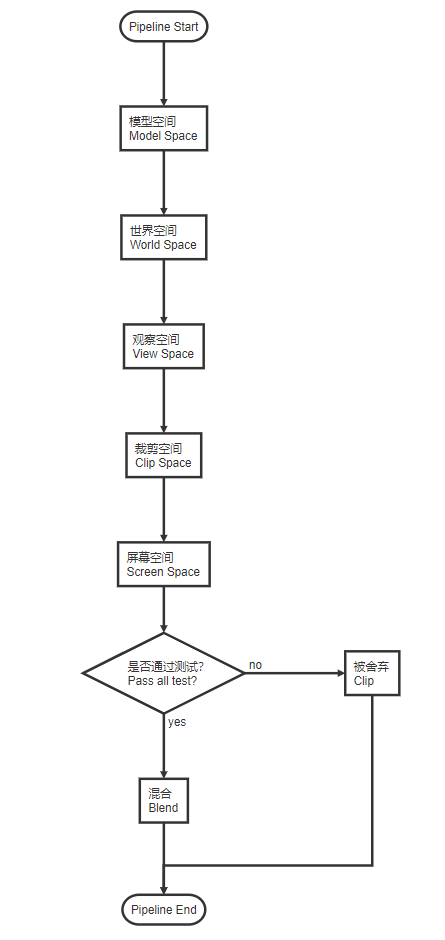
经过上述的步骤,模型中的顶点就正式被渲染到了显示器的像素上。