RayMarching+BasicLighting

Posted on 2021-11-02 Edited on 2021-11-14 In 技术向

Ray Marching & Basic Lighting

最近去学习了一下Ray marching相关的知识，虽然仅仅是一个入门。于是我准备将raymarching和基础的光照模型放在一篇文章里学习记录一下。

Ray Marching（光线步进）

Ray Marching概念

先从Ray marching开始讲起，从名字可以看出，raymarching是一个模拟光线不断前进的过程。
我们想象从观察点（人眼或者相机）开始，对视线范围内的每一个方向都发射一条射线（Ray），那么这条射线如果与某样物体相交，则这个方向上我们需要绘制这个物体，最终当我们对每条射线都这样检查完毕时，所有相交点都绘制完毕了（对于计算机来说，这里的“每条射线”就变成了从相机到屏幕每个像素的方向射线）。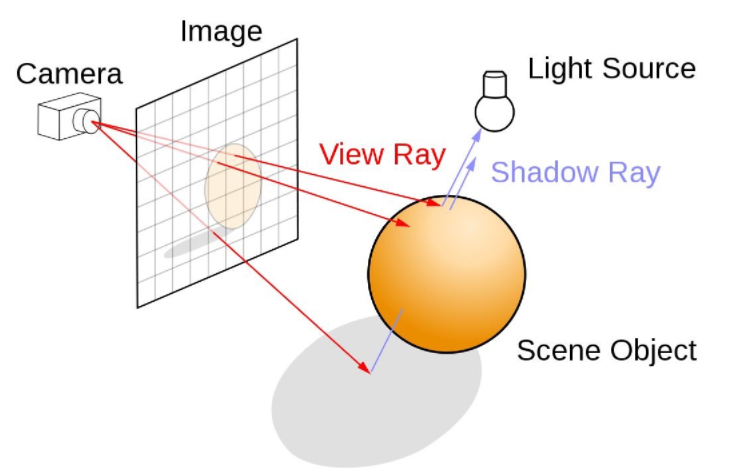

判断相交

显然，这里我们会遇到一个问题，就是如何判断射线是否与某样物体相交。在raymarching中，我们采用找最短距离步进的方式来计算，即，对于一个物体，我们每次沿射线步进的距离是从该点到该物体的最短距离，这样我们就保证了，在这个步进半径内的任何一个点，都不会出现在该物体的内部。当我们某一次寻找该距离的值小于阈值时，我们就判断这个射线方向与物体相交，当总距离大于最大阈值时，我们判断这条射线方向没有物体。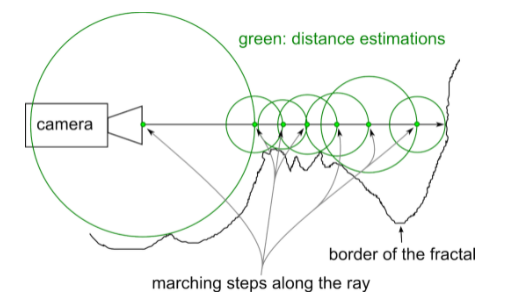

大体代码实现如下：

float RayMarching(float3 rayOrigin, float3 rayDir)
{
	float total = 0.0f;
    for(int i = 0; i < MAX_ITERATION; i++)
    {
    	if(total > MAX_DISTANCE)
    	{
    		return -1.0f;
    	}
		float3 pos = rayOrigin + rayDir * total;
		float distance = GetDistance(pos);
		
		total += distance;
		
		if(distance < MIN_DISTANCE)
		{
			return total;
		}
    }
    return -1.0f;
}

这里我们会遇到第二个问题，就是代码中的GetDistance函数，我们如何知道某一点到某物体的最短距离呢，这里需要用到有符号距离场（Signed Distance Field, SDF）来计算。

有符号距离场（SDF）

有符号距离场可以看做一个对空间的表达函数，我们用一个方式来表达离某一点最近的空间距离（一般是一个标量场函数或一张立体纹理）。似乎SDF可以用来做AO（环境光遮蔽）和软阴影（Soft Shadow），如UE4，但是目前没有学习到，留个（TODO）。
在raymarching中，我们使用标量场函数来计算某点到物体的最短距离，这里拿最简单的球体来举例。我们有$Param_{Sphere} = (x, y, z, w)$，这里记作S，其xyz分量为球心坐标，w分量为球的半径，又有$位置P(x,y,z)$，显然，从位置P到球S的最短距离为$\sqrt{(P.x - S.x)^2 + (P.y - S.y)^2 + (P.z - S.z)^2} - w$。
所以我们可以得到球体的标量场函数如下

float SDF_Sphere(float3 pos, float4 param)
{
	return length(pos - param.xyz) - param.w;
}

除了球体，还有许多不同的标量场函数，如锥体、长方体、甜甜圈等，具体可以看📌InigoQuilez大佬的文章

SDF的其它计算

上述标量场函数仅仅是单个几何体的表达，通过对不同标量场的计算，我们可以得到多个几何体的布尔运算结果，如交集、差集、并集等。
这里仍然以最简单的交集为例，我们只需要将两个SDF函数的结果求得最小值即可，代码如下

float Operation_Union(float sdf1, float sdf2)
{
	return min(sdf1, sdf2);
}

此外，还有一些复杂的计算如平滑过渡的并集（Smooth Union）等算法，均可以在上述IQ的文章中找到。

SDF的其他应用

了解SDF之后，我们可以在raymarching的时候做一些trick来实现一些有趣的效果，如我们对raymarching时传入的位置坐标做周期性的取模，遍可以实现无限循环的模型效果，如下图所示，我将距离函数$f(x)=x$转换为周期为a的函数，即可以对空间内每一个$a^3$的立方体进行SDF计算，从而得到无限的空间。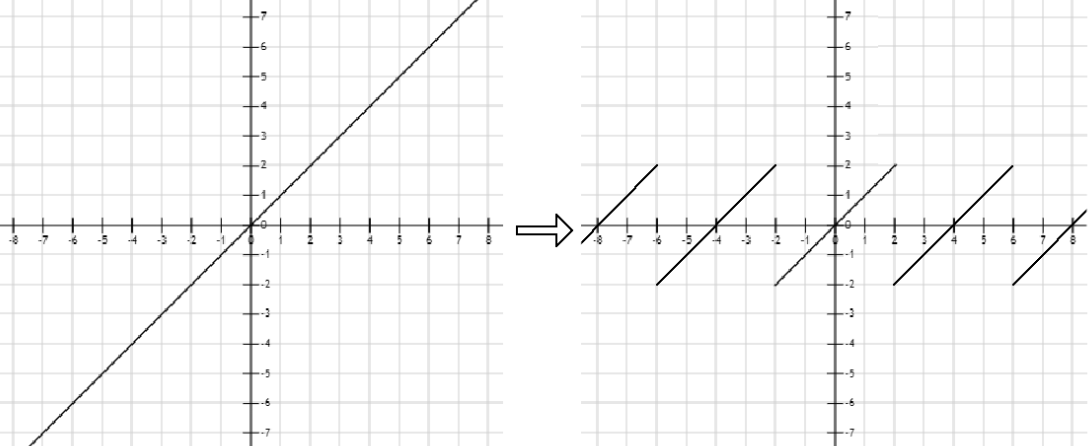

如下图是对一个球体和立方体求差集后对齐周期性采样的结果

可以看到raymarching通过对SDF的简单计算便可以得到强大的结果。这里我是参考于📌油管上对ray marching的一个详细教程。

着色（Shading）

在使用射线以及SDF处理完几何信息之后，我们需要对得到的几何信息（对应在计算机屏幕上则为像素）进行着色，这里我将使用最基础的光照模型来进行raymarching下着色的说明。

计算法线

在基础光照模型中我们对光的计算离不开几何体的表面法线，在一般的渲染流程中，法线信息通常来源于模型的顶点信息或是法线贴图，在raymarching中，我们没有这两个信息，因此需要自己计算表面法线。
这里我们通过求梯度的公式来获得表面法线，即计算点$P(x,y,z)$在三个坐标轴方向上SDF函数值的偏导，来得到该点的法线方向。
$n = normalize(\nabla f(p))$
$\nabla f(p) =\begin{Bmatrix} \frac{df(p)}{dx}, \frac{df(p)}{dy}, \frac{df(p)}{dz} \end{Bmatrix}$
$\frac{df(p)}{dx} \simeq \frac{f(p + (h, 0, 0)) - f(p)}{h}$

如上所示，我们便完成了raymarching某交点（屏幕像素）的法线计算，用代码简单计算如下：

float2 tinyVal = float2(0.00001, 0.0);
float3 normal = float3
(
	GetDistance(pos + tinyVal.xyy) - GetDistance(pos),
	GetDistance(pos + tinyVal.yxy) - GetDistance(pos),
	GetDistance(pos + tinyVal.yyx) - GetDistance(pos)
);
return normalize(normal);

Lambert漫反射模型

这里我们使用基础的Lambert模型来计算漫反射，以平行光为例，我们认为从光源出射的光线在单位面积上的辐照度来表示，那么当光线是斜着入射到物体表面时，相同辐照度反应在物体表面的面积就增大了，因此亮度也会相应地降低，这里我们可以用表面法线与光线入射方向的点积来计算这个差异，如下图所示。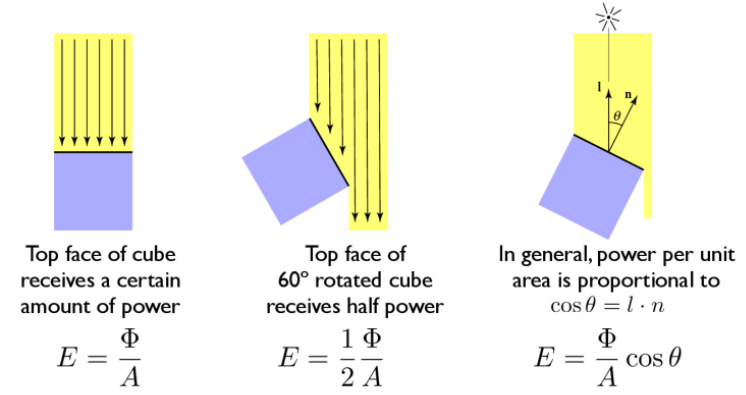

这里需要注意的是，对于模型背面的点，其法线与入射光方向的点积结果为负数，在图形学中负数对于颜色的影响与0一样（均为黑色），但是为了让后续的计算不出现问题，我们对结果取非负处理，因此最终漫反射颜色计算公式为
$C_{diffuse} = max(0, dot(normal, lightDir)) * C_{light} * I_{light}$
其中C为颜色，I为入射光辐照度。

半Lambert漫反射模型

从上述公式可以看出，Lambert漫反射模型会让模型背向光源的一半完全呈现黑色（因为点积为负），因此出现了半Lambert模型，其计算也很简单，即把上述公式中的max()部分改变为：
$dot(normal, lightDir) * 0.5 + 0.5$
即
$C_{diffuse} = (dot(normal, lightDir) * 0.5 + 0.5) * C_{light} * I_{light}$
我们将两者的函数图像及实际效果作比较，可以看出半Lambert模型的结果会比前者拥有更多层次。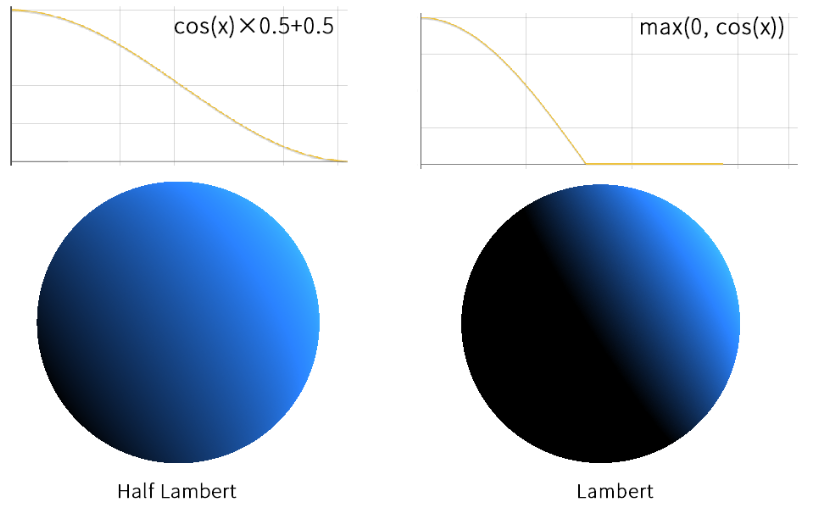

Blinn-Phong高光模型

对于一些表面光滑的物体，除了漫反射，我们还需要高光反射，光线能够大部分经过法线而反射到我们的观察点（如相机）。
最基础的高光模型是Phong式算法，我们将入射光方向经过法线反射的方向与观察方向做点积，这样越接近恰好反射到观察点的表面位置，高光越强，如下图所示：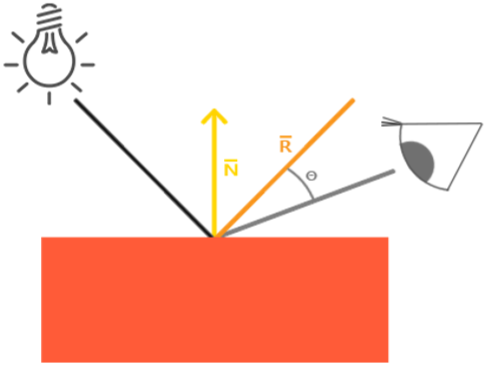

但是这个方法当观察方向与入射光方向在法线同侧时，反射方向与观察方向的夹角将会大于90°，导致点积为负数，这样当相机转到某一个角度时，会出现高光突然消失的情况，这是我们不希望看到的，于是便有了Blinn-Phong高光模型。
在Phong式模型的基础上，我们计算了中间向量H，它是入射光方向与视线方向的平均，我们用向量H与法线N求点积，这样就保证了H和N的夹角永远不会大于90°，如下图所示：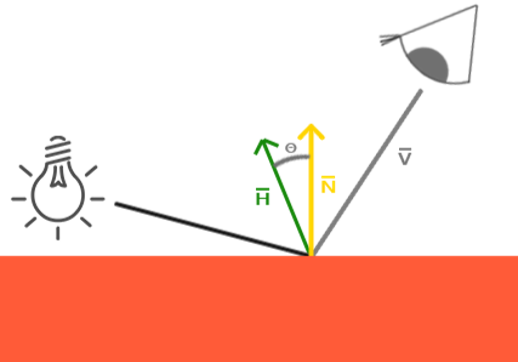

如果直接求得点积，那么cos函数的变化会太过平滑，导致我们不希望看到的高光面积过于大的情况，因此我们引入一个新的变量shininess，来对点积结果进行次幂操作，来缩小高光的面积。因此最终，我们能够得到高光的计算公式；
$C_{specular} = pow(max(0, dot(H, N)), shininess) · C_{light} · I_{light}$
计算完高光后，我们可以得到如下的效果：

可以看到随着角度、和shininess的变化，高光的强度和范围都会发生相应的变化。

结果合并

在得到了漫反射（Diffuse）和高光（Specular）之后，我们便可以将他们相加后乘以物体的固有色，得到基础光照的最终结果$C_{final}=C_{origin}·C_{light}·I_{light}·(P_{diffuse} + P_{specular})$

深度缓存与遮挡

到目前为止，我们已经得到了屏幕每个像素的颜色，但是这里仅仅是获得了通过raymarching渲染得到的像素颜色，如果场景中还存在其余渲染结果，如最普遍的Forwardbase Rendering或Deferred Rendering等，则我们会得到不正确的结果，如下图所示

我在场景中放置了一个立方体，该立方体是用前向渲染（Forwardbase Rendering）完成渲染的，但是当旋转相机的时候，本应该挡住球体的立方体，被渲染在了球体之后，看起来就变得十分怪异。
为了解决这个问题，我们需要用到深度缓存，在进行画面渲染的时候，为了保证越靠近镜头的物体被渲染在越前面，我们需要用到一些算法，譬如画家算法（已经不再使用）或者深度缓存（Depth Buffer）。
深度缓存为屏幕上的每一个像素都存储了一个深度值，该深度值的取值为[0, 1]，我们可以将一个场景的深度缓存中的值输出为颜色，如下图，可以看到，越靠近相机的颜色越接近黑色，这是因为从近到远，深度值是从0到1。

我们将该深度值乘以相机视椎体的远平面，便可以得到[0, Far]取值的深度值，也就是说，我们得到了屏幕上每一个像素最接近相机的物体的距离，于是我们可以将该距离与raymarching的结果相比，便可以得到遮挡关系，如下图是加入了深度值比较后的正确结果

在代码实现上看，我们仅需把前文中RayMarching函数的判断部分增加上与深度值的比较即可，如下

if(total > MAX_DISTANCE || total >= depth)
{
	return -1.0f;
}

硬阴影与软阴影

到目前，我们已经解决了排序问题和着色问题，现在我们创建几个SDF函数，分别是由两个球体和一个立方体交并运算得到的几何体，和一个平面，我们将他们求并集，得到的结果如下：

可以看到，虽然我将几何体放置在了平面的正上方，但是看上去仍然像是“漂浮”在平面之上，其中一个重要原因是这里缺少了投影。对于前向渲染等，展示投影的方式有譬如Shadow Map等。但是在Ray Marching中，我们可以更加方便地得到投影。

再次使用文章开头的这张图，但是这次我们关注的是图中右边蓝色标注的Shadow Ray，在raymarching中，我们如果想得到一个像素是否处于阴影中，我们只需要从该处，向光源方向再做一次Ray Marching，如果射线与物体相交，则说明该像素处于阴影中，反之则不在阴影中，代码表示如下。

float HardShadow(float3 ro, float3 rd, float maxDis, float minDis)
{
	for(float t = minDis; t < maxDis;)
	{
		float dis = GetDistance(ro + rd * t);
		// Hit something
		if(dis < minDis * 0.5)
		{
			return 0.0;
		}
		t += dis;
	}	
	return 1.0;
}

注意这里我们传入的ro（Ray Origin），需要加上一个微小的偏移，一般是沿法线方向偏移一个极小的值，因为直接代入某点的话，该点已经处在某个几何体上，其GetDistance的结果就为0。
现在我们拥有了基础的阴影计算结果，把它代入到我们的着色函数中，可以得到如下图结果：

从结果中可以看出，阴影正确地投影在了地面以及几何体自身。但是这个阴影的结果有些锋利，其边缘非常硬（Hard Shadow），为了得到一个更柔化的边缘，我们可以在上述函数的基础上做出一些修改，来得到软阴影（Soft Shadow）。
在raymarching中获得软阴影的思想是，对于没有被遮挡的像素，我们找到步进过程中，最靠近几何体的采样点，占总采样距离的比例的最小值。这样，稍偏离硬阴影的部分，其软阴影也最强。原理如下图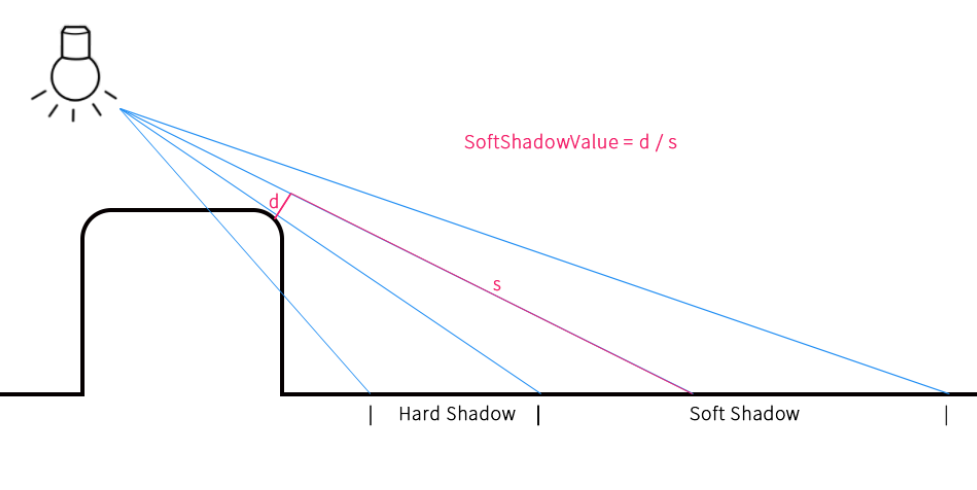

代码如下

float SoftShadow(float3 ro, float3 rd, float maxDis, float minDis, float k)
{
	float result = 1.0;
	for(float t = minDis; t < maxDis;)
	{
        float dis = GetDistance(ro + rd * t);
        // Hit something
        if(dis < minDis * 0.5)
        {
            return 0.0;
        }
        result = min(result, k * dis / t);
        t += dis;
	}
	return result;
}

其中k为调整参数，k越小，result值越小，软阴影效果越强。
通过调整k参数，我们可以得到软阴影的效果如下图

AO环境光遮蔽

有了阴影，我们的几何体看上去更像是被放在了地面上，但是我们还可以做到更多，譬如看如下图的位置，在现实世界中，如墙角等垂直的平面上，都会比周围的亮度更低，而我们现在的结果还没有展现这一点。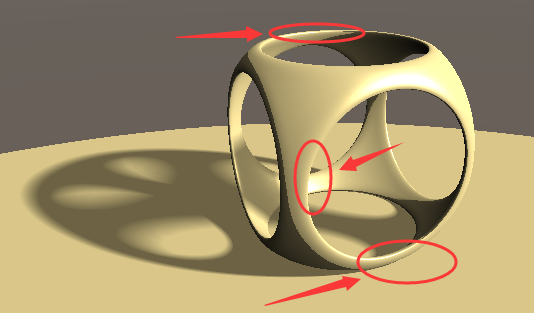

这里我们可以使用环境光遮蔽（Ambient Occlusion）技术来实现这一点。
AO的定义如下：AO是来描绘物体和物体相交或靠近的时候遮挡周围漫反射光线的效果，可以解决或改善漏光、飘和阴影不实等问题，解决或改善场景中缝隙、褶皱与墙角、角线以及细小物体等的表现不清晰问题，综合改善细节尤其是暗部阴影，增强空间的层次感、真实感，同时加强和改善画面明暗对比，增强画面的艺术性。
如下图，AO让老人脸上的皱纹等区域的亮度减少，显得层次感比原图更加丰富。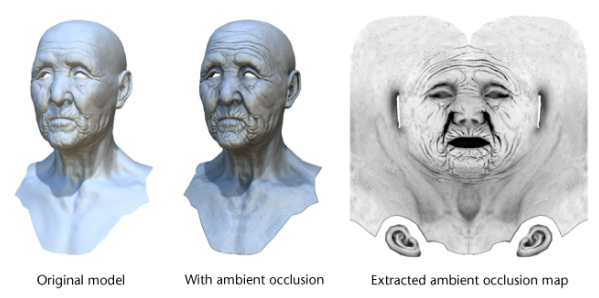

本文中我们只讨论RayMarching下的AO实现，我们沿着法线方向一点点步进，每个点使用GetDistance采样一次，并把结果和步进总距离作比较，可以想象，当某像素的周围有其它遮挡物时，GetDistance的结果会比步进距离小，而当某像素的周围一片空旷时，GetDistance的结果和步进距离是相同的。我们可以用代码实现如下：

float AmbientOcclusion(float3 pos, float3 normal)
{
	float ao = 0.0;
	float dist = 0.0;
	for(int i = 1; i <= _AoIteration; i++)
	{
		dist = _AoStep * i;
		ao += max(0.0, (dist - GetDistance(pos + normal * dist)) / dist);
	} 
	return 1 - ao * _AoIntensity;
}

这里我将AO的计算结果直接作为颜色输出，得到如下结果：

可以看见，缝隙、细小处的阴影也被完整表达了。

总结

至此，我们把raymarching和光照等结果都处理完毕了，我们把每一步的结果拆解表达如下。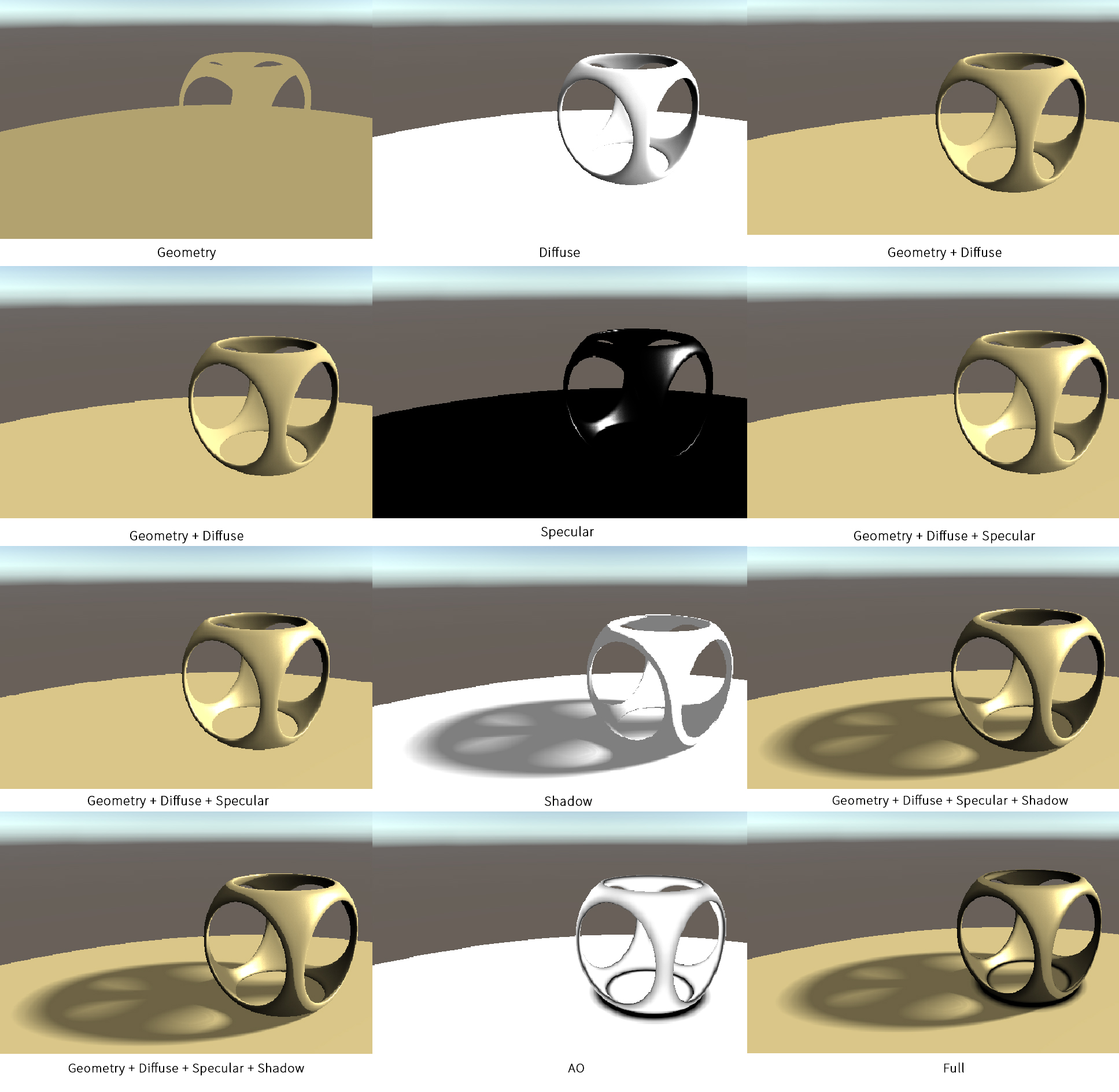

Ray Marching在实时渲染的领域中常常被用来处理体积相关的画面效果，如体积光（Volumetric Light），云等。
有关体积光和云等的效果的实现将用单独的文章来介绍。
此外，在ShaderToy上还有许多出色的艺术家使用RayMarching来实现惊人的几何和光照等效果，如📌IQ大佬用RM实现的实时渲染蜗牛，都是非常优秀的效果。